Synopsis
Data
In this page, I’m going to analyze the ToothGrowth data in the R datasets package.
ToothGrowth data set contains the result from an experiment studying the effect of vitamin C on tooth growth in 60 Guinea pigs. Each animal received one of three dose levels of vitamin C (0.5, 1, and 2 mg/day) by one of two delivery methods, (orange juice or ascorbic acid (a form of vitamin C and coded as VC).
This data set contain three columns.
-
len: Tooth length -
supp: Supplement type (it has 2 type, VC for Vitamin C and OJ for Orange Juice) -
dose: Dose of supplement given per mg in 1 day
Processing Steps
-
Load the ToothGrowth data and perform some basic exploratory data analyses
-
Provide a basic summary of the data.
- Use confidence intervals and/or hypothesis tests to compare tooth growth by supp and dose.
- State conclusions and the assumptions.
Loading and Preprocessing Data
Loading the data set
data <- data.frame(ToothGrowth)
Showing some observations and the structure of the data set
# showing the first 5 observations
head(data)
| len | supp | dose |
|---|---|---|
| 4.2 | VC | 0.5 |
| 11.5 | VC | 0.5 |
| 7.3 | VC | 0.5 |
| 5.8 | VC | 0.5 |
| 6.4 | VC | 0.5 |
| 10.0 | VC | 0.5 |
# showing the last 5 observations
tail(data)
| len | supp | dose | |
|---|---|---|---|
| 55 | 24.8 | OJ | 2 |
| 56 | 30.9 | OJ | 2 |
| 57 | 26.4 | OJ | 2 |
| 58 | 27.3 | OJ | 2 |
| 59 | 29.4 | OJ | 2 |
| 60 | 23.0 | OJ | 2 |
# showing data set structure
str(data)
'data.frame': 60 obs. of 3 variables:
$ len : num 4.2 11.5 7.3 5.8 6.4 10 11.2 11.2 5.2 7 ...
$ supp: Factor w/ 2 levels "OJ","VC": 2 2 2 2 2 2 2 2 2 2 ...
$ dose: num 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 ...
From the result above, we have 60 Observations and 3 variables.
len and dose are numerical value. len is the dependent variable of the experiment, . Otherwise, dose is the one of the control variable of the experiment. Let’s see how many unique value in dose
unique(data$dose)
0.5
1
2
There are 3 different treatment about dosage of the supplement are given, which are 0.5, 1.0, and 2.0. Also, there 2 different treatment on the type of supplement are given.
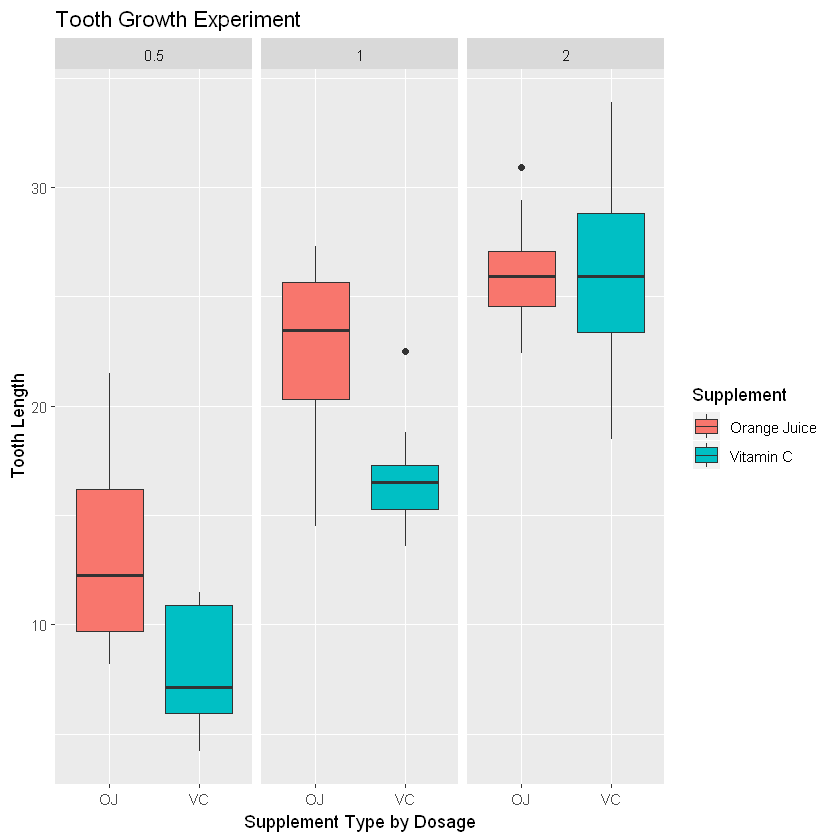
Showing plot of the experiment result.
# import necessary library
library(ggplot2)
# create a box plot
ggplot(data, aes(x=supp, y=len, fill=supp)) +
geom_boxplot() +
facet_wrap(~dose) +
labs(title = "Tooth Growth Experiment", x = "Supplement Type by Dosage", y = "Tooth Length") +
scale_fill_discrete(name = "Supplement", breaks = c("OJ", "VC"),
labels = c("Orange Juice", "Vitamin C"))
Data Analysis
The data analysis examine by using statistical t-test. We will run 4 t-test analysis, one by supp factor variable and 3 by dose treatment. We will see the p-value and Confidence Interval.
t-test by Supplement
with(data,
t.test(len~supp, paired = F, var.equal = F))
Welch Two Sample t-test
data: len by supp
t = 1.9153, df = 55.309, p-value = 0.06063
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.1710156 7.5710156
sample estimates:
mean in group OJ mean in group VC
20.66333 16.96333
We see that p-value is 0.06 (greater that 0.05) and the confidence interval is contain 0. So, we can reject the null hypotheses. There is no significant statistical difference in supplement treatment.
t-test by Dose
with(data,
t.test(len[dose == 1.0],
len[dose == 0.5],
paired = F, var.equal = F))
Welch Two Sample t-test
data: len[dose == 1] and len[dose == 0.5]
t = 6.4766, df = 37.986, p-value = 1.268e-07
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
6.276219 11.983781
sample estimates:
mean of x mean of y
19.735 10.605
with(data,
t.test(len[dose == 2.0],
len[dose == 1.0],
paired = F, var.equal = F))
Welch Two Sample t-test
data: len[dose == 2] and len[dose == 1]
t = 4.9005, df = 37.101, p-value = 1.906e-05
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
3.733519 8.996481
sample estimates:
mean of x mean of y
26.100 19.735
with(data,
t.test(len[dose == 2.0],
len[dose == 0.5],
paired = F, var.equal = F))
Welch Two Sample t-test
data: len[dose == 2] and len[dose == 0.5]
t = 11.799, df = 36.883, p-value = 4.398e-14
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
12.83383 18.15617
sample estimates:
mean of x mean of y
26.100 10.605
We see that all combinations of dosage level analysis has very small p-value and lower that 0.05. So, we have not enough evidence to reject the null hypotheses. There are statistically significant difference to all combinations of dosage level that give a positive effect to tooth growth.
Conclusions
From the result of Data Analysis section, we conclude that :
- It seem the type of supplement doesn’t give any effect to subjects tooth growth.
- The level of supplement dosages give effect to subjects tooth growth. Its mean that the increase of thee dosage level can stimulate subject’s tooth to grow more.